Introduction
Radial Basis Function interpolation can be expressed as a system of linear equations of the form Ax = v where
Ax = v \quad\Leftrightarrow\quad
\begin{bmatrix}
a_{11} & a_{12} & a_{13} & \dots & a_{1n} \\[0.5em]
a_{21} & a_{22} & a_{23} & \dots & a_{2n} \\[0.5em]
\vdots & \vdots & \vdots & \ddots & \vdots \\[0.5em]
a_{n1} & a_{n2} & a_{n3} & \dots & a_{nn}
\end{bmatrix}
\begin{bmatrix}
x_1 \\[0.5em]
x_2 \\[0.5em]
\vdots \\[0.5em]
x_n
\end{bmatrix}
=
\begin{bmatrix}
v_1 \\[0.5em]
v_2 \\[0.5em]
\vdots \\[0.5em]
v_n
\end{bmatrix}
- The interpolation matrix A stores the distances between all of the source points. It has a row for each source point and respective column entries of the distances to all the other source points. Imagine strings connecting each point to each point, we’ll have to measure their lengths and store those in A.
- The unknown matrix x contains the weights / coefficients of each point. Since the linear combination of A and x results in v, finding x will enable us to generate new values for arbitrary positions. Keep in mind that A grows exponentially with the amount of source points, hence solving for x will become more expensive at the same rate.
- The attribute values of each point are contained in matrix v, it is the same size as coefficient matrix x (pointcount*attrib_size) eg. 100×3 for 100 source points with a float3 attribute.
We can construct matrices A and v from known data (point positions & attrib. values), then use a linear matrix solver to obtain the weight/coefficient matrix x. For the solving we’ll rely on Python module NumPy since it is packaged with Houdini.
Preparation
First of all let’s create a set of source points carrying an attribute we want to interpolate. We’ll need something to sample from afterall. I’m using a box with divisions but it could be any unconnected point cloud. Then we may use eg. a bend deformer and a point wrangle to calculate the deformation attribute with this one-liner.
v@def = point(1, "P", @ptnum) - @P;
It might seem weird to capture a deformer that could just straight be used on geometry, but that way we’ll have a ground truth sample for comparison. You could use any other method to generate an attribute of any type (with respective adjustments to the types used for v, x and @def in the code) on the lookup points.
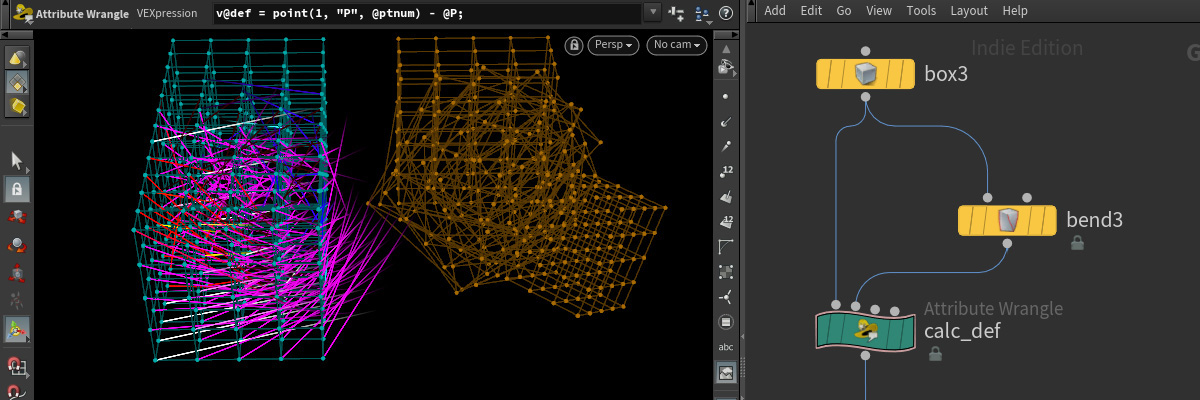
Now theres points with an attribute to interpolate from. We could just do the whole RBF calculation for every point of the to-be-deformed geometry, which would be pretty expensive when run over dense geo. Fortunately we can decouple solving for the coefficients and geometry deformation, which will use more memory (to store the coef matrix) but is a lot faster. We’re also not bound to do the deformation in Python and can use OpenCL or VEX instead.


